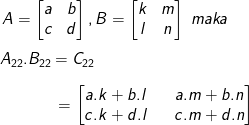materi pelajaran matematika yang disukai: August 2020

Pengertian Matriks

Matriks adalah kumpulan bilangan yang disusun secara baris atau kolom atau kedua-duanya dan di dalam suatu tanda kurung. Bilangan-bilangan yang membentuk suatu matriks disebut sebagai elemen-elemen matriks. Matriks digunakan untuk menyederhanakan penyampaian data, sehingga mudah untuk diolah.

Diketahui jumlah penjualan mobil jenis A, B, dan C, dengan harga jual masing-masing 146, 275, dan 528 (dalam juta) pada kota-kota P, Q, R, adalah :

JENIS MOBIL	HARGA MOBIL (JUTA)	JUMLAH PENJUALAN TIAP KOTA (UNIT)
JENIS MOBIL	HARGA MOBIL (JUTA)	KOTA P	KOTA Q	KOTA R
A	146	34	56	41
B	275	45	36	37
C	528	51	32	46

Data penjualan mobil tersebut dapat dibuat dalam bentuk matriks sebagai berikut :

Matriks harga mobil adalah $\begin{pmatrix} 146 \\ 275 \\ 528 \end{pmatrix}$
Matriks jumlah penjualan adalah $\begin{pmatrix} 34 & 56 & 41 \\ 45 & 36 & 37 \\ 51 & 32 & 46 \end{pmatrix}$

Lebih sederhana bukan?

Ordo Matriks

Dijelaskan sebelumnya matriks terdiri dari unsur-unsur yang tersusun secara baris dan kolom. Jika banyak baris suatu matriks adalah m, dan banyak kolom suatu matriks adalah n, maka matriks tersebut memiliki ordo matriks atau ukuran m x n. Perlu diingat bahwa m dan n hanya sebuah notasi, sehingga tidak boleh dilakukan sebuah perhitungan (penjumlahan, perkalian). Pada contoh matriks jumlah penjualan mobil diatas diketahui bahwa:

pengertian dan ordo matriks

Banyak baris, m = 3
Banyak kolom, n = 3
Ordo matriks, m x n = 3 x 3

Penamaan/notasi matriks menggunakan huruf kapital, sedangkan elemen-elemen di dalamnya dinotasikan dengan huruf kecil sesuai dengan penamaan matriks dan diberi indeks ij. Indeks tersebut menyatakan posisi elemen matriks, yaitu pada baris i dan kolom j. Sebagai contoh, matriks sebelumnya untuk penjualan mobil:

$E = \begin{pmatrix} e_{11} & e_{12} & e_{13} \\ e_{21} & e_{22} & e_{23} \\ e_{31} & e_{32} & e_{33} \end{pmatrix} = \begin{pmatrix} 34 & 56 & 41 \\ 45 & 36 & 37 \\ 51 & 32 & 46 \end{pmatrix}$

Dimana, $e_{12} = 56$ adalah elemen matriks yang berada pada baris ke-1 (i = 1) dan kolom ke-2 (j = 2). Begitu juga dengan elemen matriks yang lainnya.

Pada matriks terdapat dua jenis diagonal, yaitu diagonal utama dan diagonal sekunder. Diagonal utama merupakan elemen-elemen dengan yang bisa membentuk garis miring. Diagonal sekunder merupakan kebalikan dari garis miring diagonal utama. Perhatikan matriks berikut:

$E = \begin{pmatrix} 34 & 56 & 41 \\ 45 & 36 & 37 \\ 51 & 32 & 46 \end{pmatrix}$

Diagonal utama adalah elemen 34, 36, 46, sedangkan diagonal sekunder adalah elemen 41, 36, 51.

Matriks Identitas

Matriks diagonal dengan elemen-elemen diagonal utamanya bernilai 1 disebut matriks identitas. Pada umumnya matriks identitas dinotasikan dengan “I”. Contoh:

$A = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}$ atau $B = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}$

Jenis-jenis Matriks

Matriks dapat dikelompokan ke beberapa jenis berdasarkan pada jumalah baris dan kolom serta pola elemen matriksnya sebagai berikut :

1. Matriks Baris dan Matriks Kolom

Matriks baris adalah suatu matriks yang hanya memiliki satu baris saja. Sedangkan, matriks kolom adalah suatu matriks yang hanya memiliki satu kolom saja. Contoh:

A = (1 4) atau B = (3 7 9) adalah matriks baris

$\begin{pmatrix} 146 \\ 275 \\ 528 \end{pmatrix}$ atau $D = \begin{pmatrix} p \\ q \end{pmatrix}$ adalah matriks kolom

2. Matriks Persegi

Matriks yang memiliki jumlah kolom dan baris yang sama disebut matriks persegi. Matriks persegi memiliki ordo n.

Contoh:

$A = \begin{pmatrix} 34 & 56 & 41 \\ 45 & 36 & 37 \\ 51 & 32 & 46 \end{pmatrix}$ adalah matriks persegi berordo 3, atau

$B = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}$ adalah matriks persegi berordo 2.

3. Matriks Segitiga Atas dan Segitiga Bawah

Matriks persegi A yang memiliki elemen matriks $a_{ij} = 0$ untuk $i > j$ atau elemen-elemen matriks dibawah diagonal utama bernilai 0 disebut matriks segitiga atas. Matriks persegi A yang memiliki elemen matiks $a_{ij} = 0$ untuk $i < j$ atau elemen-elemen matriks diatas diagonal utama bernilai 0 disebut matriks segitiga bawah.

Contoh:

$A = \begin{pmatrix} 1 & 6 & 4 \\ 0 & 3 & 7 \\ 0 & 0 & 4 \end{pmatrix}$ adalah matriks segitiga atas,

$B = \begin{pmatrix} 1 & 0 & 0 \\ 7 & 3 & 0 \\ 4 & 6 & 4 \end{pmatrix}$ adalah matriks segitiga bawah.

4. Matriks Diagonal

Matriks persegi A yang memiliki elemen matiks $a_{ij} = 0$ untuk $i \neq j$ atau elemen-elemen matriks diluar diagonal utama bernilai 0 disebut matriks diagonal.

Contoh:

$A = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 4 \end{pmatrix}$ atau $B = \begin{pmatrix} 1 & 0 \\ 0 & 4 \end{pmatrix}$

5. Matriks Skalar

Matriks diagonal yang memiliki elemen-elemen pada diagonal utamanya bernilai sama disebut matriks skalar.

Contoh:

$A = \begin{pmatrix} 3 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 3 \end{pmatrix}$ atau $B = \begin{pmatrix} 4 & 0 \\ 0 & 4 \end{pmatrix}$

6. Matriks Indentitas

Sudah dijelaskan di atas.

7. Matriks Simetris

Matriks persegi A yang memiliki elemen matiks baris ke-I sama dengan elemen matriks kolom ke-j untuk i = j disebut simetris. Atau, dapat dikatakan elemen $a_{ij}$ sama dengan elemen $a_{ji}$ .

Contoh:

$\begin{pmatrix} 1 & 2 & 4 \\ 2 & 3 & 5 \\ 4 & 5 & 7 \end{pmatrix}$

Dapat dilihat bahwa elemen baris ke-1 sama dengan kolom ke-1, baris ke-2 sama dengan kolom ke-2, dan baris ke-3 sama dengan kolom ke-3.

Transpose Matriks

Transpose matriks merupakan perubahan baris menjadi kolom dan sebaliknya. Transpose matriks dari $A_{m x n}$ adalah sebuah matriks dengan ukuran (n x m) dan bernotasi AT. Jika matriks A ditanspose, maka baris 1 menjadi kolom 1, baris 2 menjadi kolom 2, dan begitu seterusnya.

Contoh:

$\begin{pmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{pmatrix}$ ditranspose menjadi $\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix}$ .

Sifat dari transpose matriks: $(A^T)^T = A$ .

Contoh Soal dan Pembahasan

Contoh Soal 1

Diketahui A = , B = , C = , Tentukan :

A + B :
A + C :

Penyelesaian :

A + B = =
A + C = tidak dapat dijumlah karena ordonya tidak sama.

Contoh Soal 2

Jika A = dan B = adalah =….

Penyelesaian :

B – A = –
B – A = =

Sifat dari penjumlahan dan pengurangan sebuah matriks yaitu :

A + B = B + A
(A + B) + C = A + (B + C)
A – B ≠ B – A

Contoh Soal 3

Jika matriks dan saling invers, tentukan nilai x !

Penyelesaian :

Diketahui bahwa kedua matriks diatas tersebut saling invers, maka berlaku syarat AA-1 = A-1A = I.

Maka :

Sehingga pada elemen baris ke-1 pada kolom ke-1 memiliki persamaan yaitu :

9(x -1) – 7x = 1
9x – 9 – 7x = 1
2x = 10
x = 5

Jadi, nilai x adalah = 5

Contoh Soal 4

OPERASI MATRIKS

1). Penjumlahan Matriks

Operasi penjumlahan dapat dilakukan pada dua buah matriks yang memiliki ukuran yang sama (ordo sama). Aturan penjumlahan matriks yaitu dengan menjumlahkan elemen-elemen yang bersesuaian pada kedua matriks.

Bentuk umum:

Contoh:

Diketahui matriks A dan matriks B. Tentukan A+B!

Jawaban:

2). Pengurangan Matriks

Operasi pengurangan dapat dilakukan pada dua buah matriks yang memiliki ukuran yang sama (ordo sama). Aturan pengurangan matriks yaitu dengan mengurangkan elemen-elemen yang bersesuaian pada kedua matriks.

Bentuk umum:

Contoh:

Diketahui matriks A dan matriks B. Tentukan A-B!

Jawaban:

3). Perkalian Matriks dengan Matriks

Perkalian matriks dapat dilakukan pada dua buah matriks yaitu jika jumlah kolomnya matriks A = jumlah baris matriks A.

Aturan perkalian matriks yaitu misalkan dimana elemen-elemen dari C (Cij) merupakan penjumlahan dari perkalian elemen-elemen A baris i dengan elemen-elemen B kolom j.

Bentuk umum 1

Bentuk umum 2

Diatas terdapat 2 versi bentuk umum, namun jangan bingung itu hanyalah untuk referensi saja. Perlu diingat, inti dari perkalian 2 matriks adalah kita harus mengalikan baris dengan kolom.

Contoh 1.1

Diketahui matriks A dan matriks B. Tentukan AB dan BA!

Jawaban:

Jadi, pada permasalahan diatas dapat disimpulkan bahwa AB $\neq$ BA.

Contoh 1.2

Buktikan apakah benar sifat asosiatif berlaku pada perkalian matriks yaitu (AB)C=A(BC)!

Jawaban:

Jadi, sifat asosiatif berlaku pada perkalian matriks yaitu (AB)C = A(BC)

4). Perkalian Matriks dengan Skalar

Suatu matriks dapat dikalikan suatu skalar k dengan aturan tiap-tiap elemen pada A dikalikan dengan k.

Bentuk umum:

Contoh:

Diketahui: k = 3, dan matriks A sebagai berikut tentukan kA!

Jawaban:

5). Trase Matriks

Misalkan A = [aij] dengan i = 1, 2, 3, ..., n dan j = 1, 2, 3, ..., n. Trase dari matriks A dinyatakan oleh trase (A), dan pada trase mmatriks ini mempunyai syarat yaitu harus matriks bujur sangkar.

Bentuk umum:

Trase A = a + e + i

Cara mencari trase dalam sebuah matriks sangatlah mudah, yaitu hanya menambahkan semua entri diagonal utama (diagonal utamanya sudah saya warnai biru).

Contoh:

Diketahui matrik A dibawah ini. Hitunglah trase A!

Jawaban:
Trase A = 1 + (-3) + 5 = 3

6). Transpose Matriks

Transpose matriks A dinotasikan

. Transpose matriks A didefinisikan sebagai matriks yang baris-barisnya merupakan kolom dari A.

Contoh:

7). Matriks Invers

Jika matriks A, dan matriks B adalah matriks bujur sangkar dan berlaku AB = BA = I (I adalah matriks identitas), maka dikatakan bahwa matriks A dapat dibalik dan matriks B adalah matriks invers dari A (dinotasikan

).

Bentuk umum:

Invers Matriks 2x2

Invers Matriks 3x3

materi pelajaran matematika yang disukai

Sunday, August 30, 2020

MATRIK, MACAM-MACAM MATRIK DAN OPERASI MATRIK

Pengertian Matriks

Ordo Matriks

Matriks Identitas

Jenis-jenis Matriks

1. Matriks Baris dan Matriks Kolom

2. Matriks Persegi

3. Matriks Segitiga Atas dan Segitiga Bawah

4. Matriks Diagonal

5. Matriks Skalar

6. Matriks Indentitas

7. Matriks Simetris

Transpose Matriks

Contoh Soal dan Pembahasan

OPERASI MATRIKS

2). Pengurangan Matriks

3). Perkalian Matriks dengan Matriks

4). Perkalian Matriks dengan Skalar

5). Trase Matriks

6). Transpose Matriks

7). Matriks Invers

Remedial PAT

Report Abuse