1. Pada segitiga ABC lancip, diketahui cos A = 4/5 dan sin B = 12/13 maka sin C = ...
Pembahasan:
jika cos A = 4/5, maka: sin A = 3/5 (didapat dari segitiga siku-siku berikut ini:
(ingat ya, bahwa cos itu samping/miring dan sin itu depan/miring)
Jika sin B = 12/13 maka cos B = 5/13 (didapat dari segitiga siku-siku berikut ini:
Maka, sin C = sin A . cos B + sin B . cos A
= 3/5 . 5/13 + 12/13 . 4/5
= 15/65 + 48/65
= 63/65
(ingat ya, bahwa cos itu samping/miring dan sin itu depan/miring)
Jika sin B = 12/13 maka cos B = 5/13 (didapat dari segitiga siku-siku berikut ini:
Maka, sin C = sin A . cos B + sin B . cos A
= 3/5 . 5/13 + 12/13 . 4/5
= 15/65 + 48/65
= 63/65
2. Dalam segitiga ABC diketahui b = 8 cm, c = 5 cm, dan sudut A = 60. Panjang sisi A = ...
pembahasan:
a² = b²+c² - 2bc.cos A
= 8²+5² - 2.8.5.cos 60
= 64 + 25 – 80 . ½
= 64 + 25 – 40
= 89 – 40
= 49
a = √49
= 7
= 64 + 25 – 40
= 89 – 40
= 49
a = √49
= 7
3. Dalam segitiga ABC jika AB = 3, AC = 4, dan <BAC = 60 maka tan <ABC = ...
pembahasan:
Perhatikan segitiga berikut:
= 9 + 16 – 12
= 13
BC = √13
Maka, kita cari nilai cos B:
= 9 + 16 – 12
= 13
BC = √13
Maka, kita cari nilai cos B:
Aplikasikan pada segitiga siku-siku:
tan <ABC = 2√3/1 = 2√3
tan <ABC = 2√3/1 = 2√3
4. Untuk 
, sin x > ½ bila ...
, sin x > ½ bila ...
pembahasan:
sin x > ½ bila berada di kuadran I dan kuadran II, maka:
5. Jika α dan β sudut lancip, tan α = ¾ dan tan β = 1 maka nilai 5(cos (α + β) + cos (α - β) adalah ...
pembahasan:
tan α = ¾, maka sin α = 3/5 dan cos α = 4/5 (gunakan segitiga siku-siku)
tan β = 1, maka sin β = ½ √2 dan cos β = ½ √2 (gunakan segitiga siku-siku)
cos (α + β) = cos α.cos β – sin α.sin β
= 4/5. ½ √2 – 3/5. ½ √2
= 4/10√2 – 3/10√2
= 1/10√2
= √2/10
cos (α - β) = cos α.cos β + sin α.sin β
= 4/5. ½ √2 + 3/5. ½ √2
= 4/10√2 + 3/10√2
= (7√2)/10
Sehingga nilai dari 5(cos (α + β) + cos (α - β) = 5 .( √2/10 + (7√2)/10 ) = 5((8√2)/10) = (40√2)/10 = 4√2
tan β = 1, maka sin β = ½ √2 dan cos β = ½ √2 (gunakan segitiga siku-siku)
cos (α + β) = cos α.cos β – sin α.sin β
= 4/5. ½ √2 – 3/5. ½ √2
= 4/10√2 – 3/10√2
= 1/10√2
= √2/10
cos (α - β) = cos α.cos β + sin α.sin β
= 4/5. ½ √2 + 3/5. ½ √2
= 4/10√2 + 3/10√2
= (7√2)/10
Sehingga nilai dari 5(cos (α + β) + cos (α - β) = 5 .( √2/10 + (7√2)/10 ) = 5((8√2)/10) = (40√2)/10 = 4√2
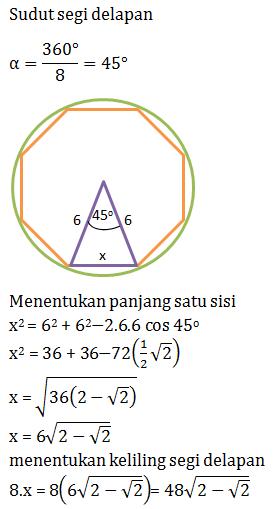
6. Panjang jari-jari luar segi delapan beraturan adalah 6 cm. keliling segi delapan tersebut adalah...
pembahasan:
7. Nilai cos 105° tan 15° adalah...
pembahasan:
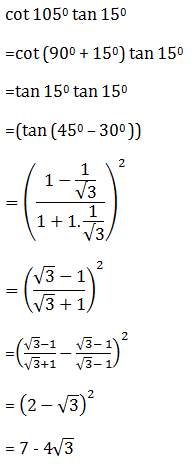
8. Diketahui sin α cos β =1/5 dan sin (α-β)=3/5 untuk 0°≤α≤180° untuk 0°≤β≤90°. Nilai sin(α+β)=...
pembahasan:
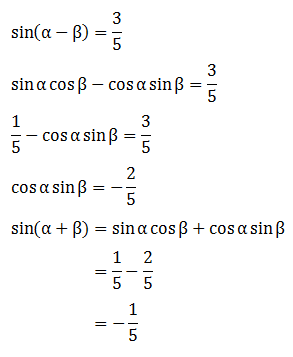
9. Grafik di atas adalah grafik fungsi ⋯⋅⋯⋅
pembahasan:
Perhatikan sketsa gambar berikut.
dari grafik sinus yang memiliki bentuk umum f(x)=asinkxf(x)=asinkx, kurva pada gambar tidak bergeser dan berawal dari titik (0,0)(0,0). Grafik juga menunjukkan bahwa nilai maksimum dan minimum fungsi adalah 44 dan −4−4, sehinggaa=N. Maksimum−N. Minimum2=4−(−4)2=4a=N. Maksimum−N. Minimum2=4−(−4)2=4
Pada saat nilai x=180∘x=180∘, fungsi kembali bernilai 00, lalu berulang kembali seperti sebelumnya, sehingga periodenya adalah 180∘180∘, dan akibatnya
k=360∘180∘=2k=360∘180∘=2
Jadi, rumus fungsi f(x)=4sin2xf(x)=4sin2x dengan batas interval 0∘≤x≤270∘
10. Perhatikan gambar dibawah ini ,
Dua orang guru dengan tinggi badan yang sama yaitu 170 cm sedang berdiri memandang puncak tiang bendera di sekolahnya. Guru pertama berdiri tepat 10 m di depan guru kedua. Jika sudut elevasi guru pertama 60∘60∘ dan guru kedua 30∘30∘ maka dapatkah anda menghitung tinggi tiang bendera tersebut...
pembahasan:
*). Ilustrasi gambar
Misalkan panjang CD = BG = xx
*). Menentukan nilai xx
Segitiga ABG :
tan60∘=ABx→AB=xtan60∘→AB=3–√xtan60∘=ABx→AB=xtan60∘→AB=3x
Segitiga ABF , substitusi AB=3–√xAB=3x
tan30∘13–√3–√.3–√x3x2xx=ABBF=3–√xx+10=x+10=x+10=10=5tan30∘=ABBF13=3xx+103.3x=x+103x=x+102x=10x=5
*). Menentukan tinggi tiang bendera (A)
AB=3–√x=3–√.5=53–√AB=3x=3.5=53
Jadi, tinggi tiang bendera adalah 53–√53 m .
*). Menentukan nilai xx
Segitiga ABG :
tan60∘=ABx→AB=xtan60∘→AB=3–√xtan60∘=ABx→AB=xtan60∘→AB=3x
Segitiga ABF , substitusi AB=3–√xAB=3x
tan30∘13–√3–√.3–√x3x2xx=ABBF=3–√xx+10=x+10=x+10=10=5tan30∘=ABBF13=3xx+103.3x=x+103x=x+102x=10x=5
*). Menentukan tinggi tiang bendera (A)
AB=3–√x=3–√.5=53–√AB=3x=3.5=53
Jadi, tinggi tiang bendera adalah 53–√53 m .
11.Sebuah gedung yang tingginya 50 m dan terdapat sebuah bola di dekat gedung. Jika sudut depresi dari puncak gedung terhadap bola adalah 30∘,30∘, maka tentukan jarak bola ke dasar gedung...
pembahasan:
*). Ilustrasi gambar gedungnya
*). Menentukan jarak bola ke dasar gedung (nilai xx ).
Perhatikan segitiga ABC, yang ditanyakan nilai xx yang merupakan sisi samping, dan diketahui sisi didepan sudut, sehingga kita menggunakan tan.
tan∠BACtan30∘13–√x=desa=BCBA=50x=50x=503–√tan∠BAC=desa=BCBAtan30∘=50x13=50xx=503
Jadi, jarak bola ke dasar gedung adalah 503–√503 m .
Perhatikan segitiga ABC, yang ditanyakan nilai xx yang merupakan sisi samping, dan diketahui sisi didepan sudut, sehingga kita menggunakan tan.
tan∠BACtan30∘13–√x=desa=BCBA=50x=50x=503–√tan∠BAC=desa=BCBAtan30∘=50x13=50xx=503
Jadi, jarak bola ke dasar gedung adalah 503–√503 m .
12. Daerah hasil fungsi Y =5-2 cos 3x adalah...
pembahasan:
13. pada segitiga ABC diketahui panjang sisi b dan sisi c berturut-turut adalah 8 cm dan 10 cm jika sudut A adalah 37°, maka tentukanlah luas segitiga tersebut..
pembahasan:
Dik: b = 8 cm, c = 10 cm, A = 37 derajat
Dit: L = ...?
L = ½ bc sin A
L= ½ (8) (10) sin 37 derajat
L= 40(3/5)
L= 24 cm
14. Dalam segitiga ABC, diketahui panjang a = 5 cm, panjang b = 8 cm. Jika besar sudut C yaitu 60o, maka tentukanlah besar sudut A...
pembahasan:
Dik : a = 5 cm, b = 8 cm, C = 60o.
Dit : A = ... ?
Mencari panjang sisi c :
⇒ c2 = a2 + b2 − 2ab cos C
⇒ c2 = 52 + 82 − 2(5)(8) cos 60o
⇒ c2 = 25 + 64 − 80(0,5)
⇒ c2 = 89 − 40
⇒ c2 = 49
⇒ c = 7 cm
Menentukan besar sudut A :
⇒ cos A = 0,785
⇒ A = 38,2o
Jadi, besar sudut A yaitu 38,2o.
Dit : A = ... ?
Mencari panjang sisi c :
⇒ c2 = a2 + b2 − 2ab cos C
⇒ c2 = 52 + 82 − 2(5)(8) cos 60o
⇒ c2 = 25 + 64 − 80(0,5)
⇒ c2 = 89 − 40
⇒ c2 = 49
⇒ c = 7 cm
Menentukan besar sudut A :
| ⇒ cos A = | b2 + c2 − a2 |
| 2bc |
| ⇒ cos A = | 82 + 72 − 52 |
| 2(8)(7) |
| ⇒ cos A = | 64 + 49 − 25 |
| 112 |
| ⇒ cos A = | 88 |
| 112 |
⇒ A = 38,2o
Jadi, besar sudut A yaitu 38,2o.
15. Diketahui sebuah segitiga ABC memiliki sisi dengan panjang a = 10 cm c = 12 cm & besar sudut B = 60̊. Hitung panjang sisi b!
pembahasan:
b2 = a2+ c2 – 2ac cos B
b2 = 100+144 – 44 cos 60̊
b2 = 244 – 44(0,5)
b2 = 244 – 22
b2 = 222
b = 14,8997
Jadi, panjang sisi b adalah 14,8997 cm
16. Diketahui sebuah segitiga ABC dengan panjang AB = 9cm dan BC = 12cm. Jika besar ∠ ABC = 30o, tentukan luas segitiga ABC!
pembahasan:
L = ½ a t
Misal a = AB, maka t adalah garis tegak lurus AB ke titik C berhadapan dengan ∠ ABC, maka
Sin ∠ABC = t/BC
t = BC × Sin ∠ABC
Sehingga diperoleh
L = ½ a t
L = ½ × AB × BC × Sin ∠ABC
L = ½ × 9cm × 12cm × Sin 30o
L = ½ × 9cm × 12cm × ½
L = 27cm2
- Misal a = BC, maka t adalah garis tegak lurus BC ke titik A berhadapan dengan ∠ ABC, maka
Sin ∠ABC = t/AB
t = AB × Sin ∠ABC
Sehingga diperoleh
L = ½ a t
L = ½ × BC × AB × Sin ∠ABC
L = ½ × 12cm × 9cm × Sin 30o
L = ½ × 12cm × 9cm × ½
L = 27cm2
Jadi, luas segitiga ABC adalah 27cm2.
17. Dalam sebuah segitiga ABC diketahui besar sudut A dan C berturut-turut yaitu 53o dan 30o. Jika panjang sisi di hadapan sudut B yaitu 6 cm, maka tentukanlah luas segitiga tersebut...
pemabahasan:
Dik : A = 53o, C = 30o, b = 6 cm
Dit : L = .... ?
Langkah pertama kita tentukan besar sudut B :
⇒ A + B + C = 180o
⇒ B = 180o - (A + C)
⇒ B = 180o - (53o + 30o)
⇒ B = 180o - 83o
⇒ B = 97o
Berdasarkan rumus di atas :
Dit : L = .... ?
Langkah pertama kita tentukan besar sudut B :
⇒ A + B + C = 180o
⇒ B = 180o - (A + C)
⇒ B = 180o - (53o + 30o)
⇒ B = 180o - 83o
⇒ B = 97o
Berdasarkan rumus di atas :
| ⇒ L = | b2 sin A sin C |
| 2 sin B |
| ⇒ L = | 62 sin 53o sin 30o |
| 2 sin 97o |
| ⇒ L = | 36 (0,8) (0,5) |
| 2 (0,99) |
| ⇒ L = | 14,4 |
| 1,98 |
⇒ L = 7,27 cm2
Jadi, luas segitiga tersebut yaitu 7,27 cm2.
Jadi, luas segitiga tersebut yaitu 7,27 cm2.
18. sebuah kapal berlayar dari pelabuhan A Ke pelabuhan B dengan kecepatan 40 km/jam selama 2jam dengan arah 30°, kemudian melanjutkan perjalanan dari pelabuhan B menuju pelabuhan C dengan kecepatan 60 km/jam selama 2-5 jam dengan arah 150°. buatlah sketsa perjalanan kapal dan tentukan jarak antara pelabuhan A dan C!
pembahasan:
Jarak = kecepatan x waktu
Jarak pelabuhan A ke B adalah 40 x 2 = 80 km
Jarak pelabuhan B ke C adalah 60 x 2,5 = 150 km
Besar sudut ABC adalah 30° + 30° = 60°
Gunakan aturan cosinus untuk mencari AC
AC² = AB² + BC² - [2 x AB x BC x cos ∠ABC]
AC² = 80² + 150² - [2 x 80 x 150 x cos 60°]
AC² = 28.900 - [2 x 80 x 150 x ¹/₂]
AC² = 28.900 - 12.000
AC = √ 16.900
Diperoleh jarak antara pelabuhan A dan C sejauh 130 km
19. Bagus berdiri dengan jarak 80 m dari sebuah menara memandang puncak menara dengan sudut elevasi 30o. Jika jarak mata Bagus dengan tanah adalah 150 cm, tinggi menara tersebut adalah ….
pembahasan:
perhatikan ilustrasi berikut.
Jadi, tinggi menara adalah
![\[ = 80 \cdot tan30^{o} + 1,5 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-2ac20231972885bd7729d40421ecfbc9_l3.png "Rendered by QuickLaTeX.com")
![\[ = 80 \cdot \frac{1}{3} \sqrt{3} + 1,5 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-54eddfa9ab7bfe9b89a5ad274fc2a9c0_l3.png "Rendered by QuickLaTeX.com")
![\[ = \left( \frac{80}{3} \sqrt{3} + 1,5 \right) \textrm{m} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-e858d56be02d212da5a3d0289b6afa39_l3.png "Rendered by QuickLaTeX.com")
20. Untuk koordinat kutub ke koordinat kartesiusJika diketahui koordinat kutub (6√3, 60°), maka koordinat kartesiusnya adalah…
pembahasan:
koordinat kutub ⇒ koordinat kartesius
(r , α) ⇒ ( x , y )
(r , α) ⇒ ( x , y )
r = 6√3 ; α = 60°
(Karena α sudut di kuadran I, maka x positif f dan y positif)
(Karena α sudut di kuadran I, maka x positif f dan y positif)
x = r cos α
⇒ 6√3 x cos 60°
⇒ 6√3 x 1/2
⇒ 3√3
⇒ 6√3 x cos 60°
⇒ 6√3 x 1/2
⇒ 3√3
y = r sin α
⇒ 6√3 x sin 60°
⇒ 6√3 x 1/2 √3
⇒ 3 x 3
⇒ 9
⇒ 6√3 x sin 60°
⇒ 6√3 x 1/2 √3
⇒ 3 x 3
⇒ 9
sehingga koordinat kartesiusnya ialah ( 3√3 , 9)
No comments:
Post a Comment