Pengertian Limit
Pada dasarnya limit digunakan untuk menyatakan sesuatu yang yang nilainya mendekati nilai tertentu, seperti tak hingga yang pada dasarnya adalah angka yang sangat besar yang nilainya tidak dapat dipastikan. Limit menjelaskan suatu fungsi jika batas tertentu didekati. Jika suatu fungsi tidak terdefinisi untuk titik tertentu, tetapi kita masih bisa mencari nilai yang didekati oleh fungsi tersebut apabila titik tertentu makin didekati yaitu dengan limit.
Rumus Limit
Dalam dunia matematika, Limit biasa di tuiskan sebagai berikut
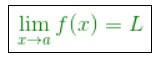
Keterangan :
- Apabila x mendekati a tetapi x tidak sama dengan a maka f(x) mendekati L
- Pendekatan x ke a bisa dilihat dari dua sisi yaitu pada sisi kiri dan sisi kanan ataupun dengan kata lain x bisa mendekati dari arah kiri dan arah kanan hingga menghasilkan limit kiri serta limit kanan.
Sifat Limit Fungsi
Jika n adalah bilangan bulat positif, k konstanta, f dan g ialah fungsi-fungsi yang memiliki limit di c, maka berlaku teorema-teorema berikut.
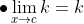
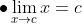
=k\lim_{x\rightarrow&space;c}f(x)\\&space;\end{align*})
+g(x)}=\lim_{x\rightarrow&space;c}f(x)+&space;\lim_{x\rightarrow&space;c}g(x)\\&space;\end{align*})
-g(x)}=\lim_{x\rightarrow&space;c}f(x)-&space;\lim_{x\rightarrow&space;c}g(x)\\&space;\end{align*})
\times&space;g(x)}=\lim_{x\rightarrow&space;c}f(x)&space;\times&space;\lim_{x\rightarrow&space;c}g(x)\\&space;\end{align*})
}{g(x)}=\frac{\lim_{x\rightarrow&space;c}{}f(x)}{\lim_{x\rightarrow&space;c}g(x)}&space;\hspace{0.1cm}&space;dengan&space;\lim_{x\rightarrow&space;c}g(x)&space;\neq&space;0&space;\end{align*})
![\begin{align*} \bullet \lim_{x\rightarrow c}[f(x)]^n=[\lim_{x\rightarrow c}f(x)]^n \end{align*}](https://latex.codecogs.com/gif.latex?\begin{align*}&space;\bullet&space;\lim_{x\rightarrow&space;c}[f(x)]^n=[\lim_{x\rightarrow&space;c}f(x)]^n&space;\end{align*})
![\begin{align*} \bullet \lim_{x\rightarrow c}\sqrt[n]{f(x)}= \sqrt[n]{\lim_{x\rightarrow c}f(x)} \hspace{0.1cm} dengan \lim_{x\rightarrow c}f(x) \geq 0 \end{align*}](https://latex.codecogs.com/gif.latex?\begin{align*}&space;\bullet&space;\lim_{x\rightarrow&space;c}\sqrt[n]{f(x)}=&space;\sqrt[n]{\lim_{x\rightarrow&space;c}f(x)}&space;\hspace{0.1cm}&space;dengan&space;\lim_{x\rightarrow&space;c}f(x)&space;\geq&space;0&space;\end{align*})
Mencari Nilai Limit
Metode ini dilakukan dengan mensubstitusi langsung nilai kedalam fungsi f(x).
Contoh Soal:
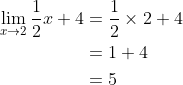
Jika pada metode substitusi menghasilkan suatu nilai bentuk tak tentu seperti:

maka fungsi tersebut harus difaktorkan terlebih dahulu, kemudian bisa disubstitusikan.
Contoh Soal:
(x+3)}{x-3}\\&space;&=\lim_{x\rightarrow&space;2}(x+3)\\&space;&=2+3\\&space;&=5&space;\end{align*})
- Metode mengalikan dengan faktor sekawan
Jika pada metode substitusi menghasilkan nilai limit yang irasional, maka fungsi dikalikan dengan akar sekawannya, kemudian bisa disubstitusikan.
Contoh Soal:
(\sqrt{x}+\sqrt{7})}{x-7}\\&space;&=\lim_{x\rightarrow&space;2}(\sqrt{x}+\sqrt{7})\\&space;&=\sqrt{7}+\sqrt{7}\\&space;&=2\sqrt{7}&space;\end{align*})
Limit Tak Hingga
Untuk menyelesaikan limit tak hingga dari suatu fungsi aljabar, terdapat dua cara yang umum digunakan, yaitu:

Contoh Soal:
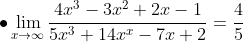
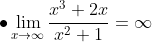

Contoh Soal:
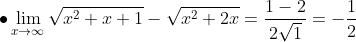
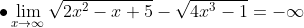
daftar pustaka :
https://www.zenius.net/blog/22841/pembahasan-limit-fungsi-beserta-limit-menuju-tak-hingga
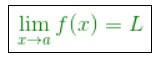




No comments:
Post a Comment