KOMPOSISI 2, 3, 4 TRANSFORMASI (GABUNGAN TRANSLASI, REFLEKSI, ROTASI, DILATASI) 1 BALOK

NAMA : M. Aydin Ramadhan (20)

KELAS : XI IPS 2

KOMPOSISI 2, 3, 4 TRANSFORMASI (GABUNGAN TRANSLASI, REFLEKSI, ROTASI, DILATASI) 1 BALOK YG TITIK KOORDINATNYA A(2,2), B(5,2), C(5,4), D(2,4), E(4,3), F(7,3), G(7,5), H(4,5) Dan perhitungan dengan perhitungan biasa dan perhitungan matriks

SOAL CERITA UNTUK MENENTUKAN NILAI OPTIMUM

 Soal Cerita untuk menentukan Nilai Optimum

1. Untuk memproduksi sepeda jenis A dengan harga jual Rp.600.000 suatu perusahaan membutuhkan biaya Rp. 200.000 dan waktu 20 jam. Sedangkan sepeda jenis B dengan harga jual Rp. 800.000 membutuhkan biaya Rp. 100.000 dengan waktu 30 jam. Jika dana yang tersedia Rp. 1.200.000 dan waktu kerja 240 jam per bulan, maka tentukanlah hasil penjualan maksimum yang diperoleh tiap bulan

Jawab :

Misalkan

x = banyaknya sepeda jenis A

y = banyaknya sepeda jenis B

maka dapat disusun kendala biaya dan waktu produksi sebagai berikut:

200000x + 100000y ≤ 1200000

20x + 30y ≤ 240

x ≥ 0

y ≥ 0

Jika disederhanakan menjadi :

2x + y ≤ 12

2x + 3y ≤ 24

x ≥ 0

y ≥ 0

Fungsi penjualan : f(x, y) = 600000x + 800000y

Selanjutnya akan dilukis grafik daerah penyelesaian sistem pertidaksamaan di atas

 

Titik A koordinatnya adalah A(0, 8)

Titik C koordinatnya adalah C(6, 0)

Sedangkan titik B merupakan perpotongan garis g dan h, diperoleh :

karena 2x + y = 12 maka 2x + 6 = 12, sehingga 2x = 6, jadi  x = 3

Jadi koordinat titik B adalah B(3, 6)

Selanjutnya titik-titik tersebut disubstitusikan ke dalam fungsi optimum yakni f(x,y) = 600000x + 800000y, sehingga diperoleh :

A(0, 8) → f(A) = 600000(0) + 800000(8) = 6.400.000

B(6, 2) → f(B) = 600000(6) + 800000(2) = 5.200.000

C(3, 6) → f(C) = 600000(3) + 800000(6) = 6.600.000

Jadi hasil penjualan maksimum yang diperoleh tiap bulan adalah Rp. 6.600.000

2. Seorang anak diharuskan memakan dua jenis tablet tiap hari. Tablet pertama mengandung 2 unit vitamin A dan 2 unit vitamin B, sedangkan tablet kedua mengandung 3 unit vitamin A dan 1 unit vitamin B. Dalam satu hari anak itu memerlukan paling sedikit 12 unit vitamin A dan 8 unit vitamin B. Jika harga tablet pertama Rp. 500 perbutir dan tablet kedua Rp. 1.000 perbutir maka agar pengeluaran minimum banyak tablet pertama yang harus dibeli adalah …

Jawab

Misalkan x = banyaknya tablet jenis pertama

y = banyaknya tablet jenis kedua

maka dapat disusun kendala kebutuhan vitamin A dan vitamin B sebagai berikut:

Dari tabel di atas dapat disusun kendala, yakni :
2x + 3y ≥ 12
2x + y ≥ 8
x ≥ 0
y ≥ 0
Fungsi pengeluaran f(x, y) = 500x + 1000y
Selanjutnya akan dilukis grafik daerah penyelesaian sistem pertidaksamaan di atas

Titik A koordinatnya adalah A(0, 8)

Titik C koordinatnya adalah C(6, 0)

Sedangkan titik B merupakan perpotongan garis g dan h, diperoleh :

karena 2x + y = 8 maka 2x + 2 = 8, sehingga 2x = 6 , x =3
Jadi koordinat titik B adalah B(3, 2)
Selanjutnya titik-titik tersebut disubstitusikan ke dalam fungsi optimum yakni f(x,y) = 500x + 1000y, sehingga diperoleh :
A(0, 8) → f(A) = 500(0) + 1000(8) = 8.000
B(3, 2) → f(B) = 500(3) + 1000(2) = 3.500
C(6, 0) → f(C) = 500(6) + 1000(0) = 3.000
Jadi besarnya pengeluaran minimum Rp. 3.000 didapat jika dibeli 6 tablet pertama

3. Seorang pedagang minuman menjual dua jenis minuman ringan pada suatu tempat yang dapat menampung 500 botol minuman. Harga beli minuman jenis A dan jenis B masing-masing Rp. 2000 dan Rp 4000 per botol. Jika ia memiliki modal Rp. 1.600.000 serta akan memperoleh laba perbuah Rp. 800 untuk minuman jenis A dan Rp. 600 untuk minuman jenis B, maka berapakah banyaknya minuman minuman jenis A dan B agar diperoleh laba maksimum ?

Jawab

Misalkan

x = banyaknya minuman jenis A

y = banyaknya minuman jenis B

maka dapat disusun kendala modal dan kapasitas kios sebagai berikut:

x + y ≤ 500

2000x + 4000y ≤ 1.600.000

x ≥ 0

y ≥ 0

Jika disederhanakan menjadi :

x + y ≤ 500

x + 2y ≤ 800

x ≥ 0

y ≥ 0

Fungsi laba : f(x, y) = 800x + 600y

Selanjutnya akan dilukis grafik daerah penyelesaian sistem pertidaksamaan di atas

Titik A koordinatnya adalah A(0, 400)

Titik C koordinatnya adalah C(500, 0)

Sedangkan titik B merupakan perpotongan garis g dan h, diperoleh :

karena x + y = 500 maka x + 300 = 500, sehingga x = 200

Jadi koordinat titik B adalah B(200, 300)

Selanjutnya titik-titik tersebut disubstitusikan ke dalam fungsi optimum yakni f(x,y) = 800x + 600y, sehingga diperoleh :

A(0, 400)     → f(A) = 800(0) + 600(400) = 240.000

B(200, 300) → f(B) = 800(200) + 600(300) = 360.000

C(500, 0)     → f(C) = 800(500) + 600(0) = 400.000

Jadi keuntungan maksimum yakni sebesar Rp. 400.000 diperoleh jika dijual minuman jenis A saja sebanyak 500 botol

SOAL TRANSFORMASI DAN PENYELESAIANNYA

 1. Bayangan garis y = 2x + 2 yang dicerminkan terhadap garis y= x adalah. . .

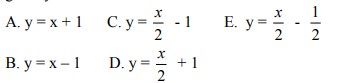
Jawaban : C

Pembahasan : 

2. Persamaan bayangan kurva y = x² – 2x – 3 oleh rotasi [0, 180°], kemudian dilanjutkan oleh pencerminan terhadap garis y = -x adalah …. 
A. y = x² – 2x – 3 
B. y = x² – 2x + 3
C. y = x² + 2x + 3
D. x = y² – 2y – 3
E. x = y² + 2y + 3

Jawaban : D

Pembahasan : 

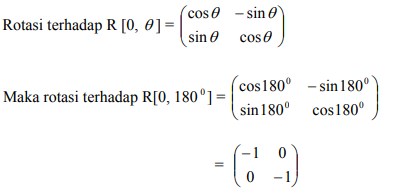
Rotasi sudut-sudut yang lain dapat dihitung sendiri menggunakan kaidah trigonometri.
pencerminan terhadap garis y = -x

3. Persamaan bayangan dari lingkaran x² +y² +4x – 6y – 3 = 0 oleh transformasi yang berkaitan dengan matriks  adalah…. 
A. x² + y² – 6x – 4y- 3 = 0
B. X² + y² – 6x + 4y- 3 = 0
C. x² + y² + 6x – 4y- 3 = 0
D. x² + y² – 4x + 6y- 3 = 0
E. x² + y² + 4x – 6y+ 3 = 0

Jawaban : A

Pembahasan : 

4. T1 dan T2 adalah transformasi yang masing-masing bersesuaian dengan 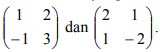Ditentukan T = T1 o T2 , maka transformasi T bersesuaian dengan matriks…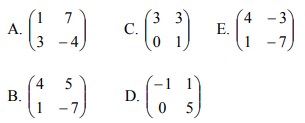

Jawaban : E

Pembahasan : 

5. Ditentukan matriks transformasi . 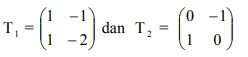Hasil transformasi titik (2,-1) terhadap T1 dilanjutkan T2 adalah…. 
A. (-4,3)
B. (-3,4)
C. (3,4)
D. (4,3)
E. (3,-4)
Jawaban : A

Pembahasan : 

6. Persamaan bayangan garis y = -6x + 3 karena transformasi oleh matriks 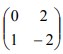  kemudian dilanjutkan dengan matriks adalah…
A. x + 2y + 3 = 0 
B. x + 2y – 3 = 0 
C. 8x – 19y + 3 = 0
D. 13x + 11y + 9 = 0
E. 13x + 11y – 9 = 0

Jawaban : E

Pembahasan : 

7. Bayangan titik A (4,1) oleh pencerminan terhadap garis x =2 dilanjutkan pencerminan terhadap garis x = 5 adalah titik…. 
A. A” (8,5) 
B. A” (10,1)
C. A” (8,1) 
D. A” (4,5)
E. A” (20,2)

Jawaban : B

Pembahasan : 

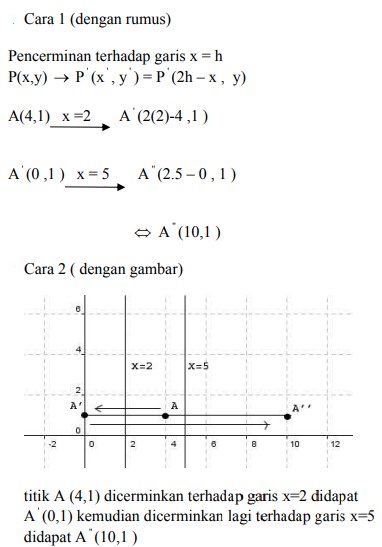
8. T1 adalah transformasi yang bersesuaian dengan matriks 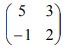 dan T2 adalah transformasi yang bersesuaian dengan matriks  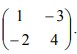Bayangan A (m,n) oleh transformasi T1 o T2 adalah (-9,7). Nilai m+n sama dengan…
A. 4
B. 5
C. 6
D. 7
E. 8 

Jawaban : B

Pembahasan : 

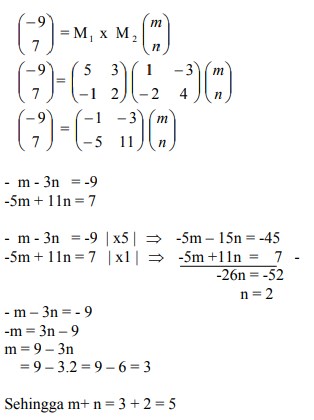
9. Bayangan ∆ABC dengan A(2,1), B(6,1), C(5,3) karena refleksi terhadap sumbu y dilanjutkan rotasi (0,90°) adalah…
A. A” (-1,-2), B” (1,6) dan C” (-3,-5)
B. A” (-1,-2), B” (1,-6) dan C” (-3,-5)
C. A” (1,-2), B” (-1,6) dan C” (-3,5)
D. A” (-1,-2), B” (-1,-6) dan C” (-3,-5)
E. A” (-1,2), B” (-1,-6) dan C” (-3,-5)

Jawaban : D

Pembahasan : 

10. Persamaan peta kurva y = x² – 3x + 2 karena pencerminan terhadap sumbu x dilanjutkan dilatasai dengan pusat O dan factor skala 3 adalah…
A. 3y + x² – 9x + 18 = 0
B. 3y – x² + 9x – 18 = 0
C. 3y – x² + 9x + 18 = 0
D. 3y + x² + 9x + 18 = 0
E. y + x² + 9x – 18 = 0 

Jawaban : A

Pembahasan : 
pencerminan terhadap sumbu x:
P ( x , y ) → P ‘ ( x , – y )
Dilatasi terhadap titik pusat O(0,0) dengan factor skala 3 :
[O, k] : P(x,y) → P'(kx, ky)
[O,3k] : P(x,y) → P'(3x, 3y)
pencerminan terhadap sumbu x dilanjutkan dilatasai
dengan pusat O dan factor skala 3 :
P(x,y) → P ‘(x, -y) → P ”(3x, -3y)

11. Luas bayangan persegipanjang PQRS dengan

P(-1,2), Q(3,2), R (3,-1), S(-1,-1)

karena dilatasi [0,3] dilanjutkan rotasi pusat O bersudut π/2 adalah…

A. 36

B. 48

C.72

D. 96

E. 108

Jawaban : E

Pembahasan : 

dilatasi [0,3] :

[O,3k] : P(x,y) → P ‘(3x, 3y)

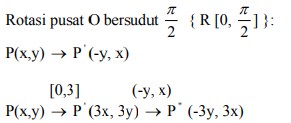
Sehingga :

P(x,y) → P” (-3y, 3x)

P(-1,2), Q(3,2), R (3,-1), S(-1,-1)

P(-1,2) → P” (-6,-3)

Q(3,2) → Q” (-6,9)

R (3,-1) → R” (3,9)

S(-1,-1) → S” (3,-3)

Buat sketsa gambarnya:

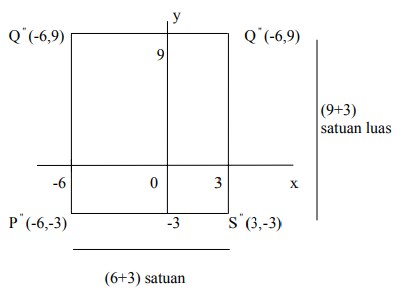
Sehingga luas transformasinya adalah :

Panjang (p) x lebar (l) = 12 x 9 = 108 satuan luas

12. Segitiga ABC dengan A(2,1), B(6,1), C(6,4) ditransformasikan dengan matriks transformasi 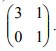 Luas bangun hasil transformasi segitiga ABC adalah….

A. 56 satuan luas 

B. 36 satuan luas

C. 28 satuan luas

D. 24 satuan luas 

E. 18 satuan luas

Jawaban : E

Pembahasan : 

misalkan T = 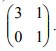maka

Luas bayangan/transformasi ∆ ABC =|det T| x luas ∆ ABC |det T| = |ad –bc| = |3-0| = 3

luas ∆ ABC :

buat sketsa gambar :

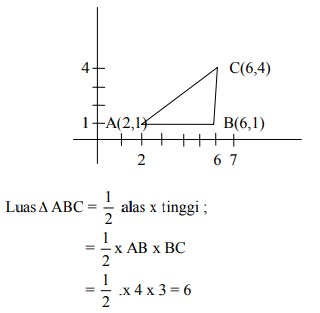
Luas bayangan/transformasi ∆ ABC =|det T| x luas ∆ ABC

= 3 x 6 = 18 satuan luas

13. Tentukan bayangan lingkaran (x-3)2 + (y+1)2 = 4 jika ditranslasikan 

 

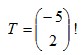
a. 5

b. 4

c. 3

d. 2

e. 1

Jawaban : B

Pembahasan : 

Ambil sembarang titik P(a,b) pada lingkaran (x-3)2 + (y+1)2 = 4 sehingga diperoleh (a-3)2 + (b+1)2 = 4

14. ABCD adalah sebuah persegi dengan koordinat titik-titik sudut A(1,1), B(2,1), C(2,2) dan D(1,2). Tentukan peta atau bayangan dari titik-titik sudut persegi itu oleh dilatasi [O,2]!

Jawaban :  

Pembahasan : 

15. Jika titik A(15,8) dicerminkan terhadap garis x=7, maka bayangan titik A adalah titik A’ dengan koordinat….

Jawaban : 

Pembahasan : 

DAFTAR PUSTAKA :  https://soalkimia.com/contoh-soal-transformasi-geometri/

SOAL DAN PEMBAHASAN MATEMATIKA SMA KELAS 11 SEMESTER GANJIL

M. Aydin Ramadhan (19) XI IPS 2

Question 1

No 1. Diketahui premis-premis berikut Premis1 Jika masyarakat mencampakkan sampah pada tempatnya maka lingkungan bersih. Premis 2: Jika lingkungan bersih maka hidup akan nyaman. Kesimpulan yang sah dari kedua premis tersebut adalah...

Jawaban :

Jika masyarakat membuang sampah pada tempatnya maka hidup akan nyaman.

No 2. Buktikan dengan induksi matematika bahwa P 1 + 3 + 5 ++ (2n-1) = n bernilai benar untuk setiap n bilangan asli. 

Jawaban :

Untuk pembuktian suatu rumus tersebut benar (berlaku), bisa kita gunakan induksi matematika, yang terdiri dari dua langkay yaitu:

Buktikan untuk n = 1 benar

Misal untuk n = k benar, akan dibuktikan untuk n = (k + 1) juga benar

Pembahasan

1 + 3 + 5 + 7 + ... + (2n – 1) = n²

Langkah pertama  

Akan dibuktikan untuk n = 1 Benar

(2n – 1) = n²

2(1) – 1 = 1²

2 – 1 = 1

1 = 1 (benar)

Langkah kedua

Misal untuk n = k benar

1 + 3 + 5 + 7 + ... + (2k – 1) = k²

Akan dibuktikan untuk n = (k + 1) juga benar

1 + 3 + 5 + 7 + .... + (2k – 1) + (2(k + 1) – 1) = (k + 1)²

|__________________|  

                     k² + (2(k + 1) – 1) = (k + 1)²

                                         k² + 2k + 2 – 1 = (k + 1)²

                                               k² + 2k + 1 = (k + 1)²

                                                     (k + 1)² = (k + 1)²

                                                          (Benar)

Jadi TERBUKTI bahwa 1 + 3 + 5 + 7 + ... + (2n – 1) = n² berlaku untuk setiap n bilangan asli.

No 3 

No 4 

Membuktikan dengan induksi matematis .

buktikan bahwa pernyataan berikut bernilai benar.

a) 1per 1.2 + 1per 2.3 + 1 per 3.4 +.... + 1 per n ( n+1 ) = n per n+ 1 untuk setiap bilangan asli

Jawaban

No 5

buktikan dengan induksi matematika bahwa a^2n-1+b^2n-1 habis dibagi oleh a+b untuk semua bilangan asli n

Jawaban

No 6

Buktikan dengan induksi matematika bahwa : 5^2n + 3n - 1 habis dibagi 9 !

Jawaban

No 7

Buktikan untuk masing masing bilangan asli n _> 5 akan berlaku 2n-3<2n-2

Jawaban

n_>5={1,2,3,4,5}

2n-3<2n-2

=2(1)-3<2(1)-2

=(-1)<0(benar)

2(2) -3<2(2) -2

=1<2 (benar)

2(3) -3<2(3) -2

=3<4(benar)

2(4) -3<2(4) -2

=5<6( benar)

2(5) -3<2(5) -2

=7<8( benar)

No 8

penyelesaian dari sistem persamaan 2x-3y=-13 dan x+2y=4 adalah?

Jawaban 

No 9

Harga 5 kg gula dan 30 kg beras adalah Rp410.000,00, sedangkan harga 2 kg gula dan 60 kg beras adalah Rp740.000,00. Harga 2 kg gula dan 5 kg beras adalah ....

Jawaban

gula = x

beras = y

5x + 30y = 410.000 |*2

2x + 60y = 740.000 |*1

10x + 60y = 820.000

2x + 60y = 740.000 

_________________-

8x = 80.000

x = 10.000

subtitusikan x nya ke persamaan

 2x + 60y = 740.000

2(10.000) + 60y = 740.000

20.000 + 60y = 740.000

60y = 720.000

y = 12.000

jadi, harga 1kg gula = Rp 10.000 dan 1kg beras = Rp 12.000

maka 2kg gula dan 5kg beras

= 2(10.000) + 5(12.000)

= 20.000 + 60.000

= Rp 80.000

No 10

Jawaban

No 11

Jawaban

Question 2

No 12

Daerah penyelesaian sistem pertidaksamaan 5x + 6y ≥ 30; -2x + y ≤ 0 ; y ≥ 2 ditunjukan oleh daerah...

Jawaban

No 13

Daerah yang diarsir pada gambar di bawah adalah himpunan penyelesaian dari sistem pertidaksamaan…

Jawaban

No 14

Tentukan nilai maksimum dari 3x + 2y yang memenuhi x + y ≤ 5 , x ≥ 0 , y ≥ 0, dan x , y ∈ R.

Jawaban

Jadi, nilai maksimum dicapai pada titik (5,0) yaitu: 3 . 5 + 2 . 0 = 15.

Question 3

No 15. Luas sebuah tempat parkir adalah 420 m2.  Tempat parkir yang diperlukan oleh sebuah sedan adalah 5 m2 dan luas rata-rata sebuah truk 15 m2.  Tempat parkir tersebut dapat meminta tidak lebih dari 60 kendaraan.  Biaya parkir untuk sedan Rp3.000.00 dan untuk sebuah truk Rp5.000,00.  Jika banyak sedan yang diparkir x buah dan banyak truk y buah, model matematika dari masalah tersebut adalah

Jawaban

sedan: x

truk: y

5x+ 15y ≤420

x+ 3y ≤84

x+y ≤60

x≥0, y≥0

maka Model:

x+ 3y ≤84 ;x+y ≤60 ; x≥0 ;y≥0

No 16 seorang penjahit memiliki persediaan 20 m kain polos dan 20 m kain bergaris untuk membuat 2 jenis pakaian. pakaian model I memerlukan 1 m kain polos dan 3 m kain bergaris.pakaian model II memerlukan 2 m kain polos dan 1 m kain bergaris.pakaian model I dijual dengan harga Rp150.000,00 per potong,dan pakaian model II dijual dengan harga Rp100.000,00 per potong.penghasilan maksimum yang dapat diperoleh penjahit tersebut adalah ....

jawaban

no 17

Diketahui matriks A = ( 2 3 -1 4 ) dan matriks B = ( 1 4 -2 5 ). Jika matriks C = 2A^t - B maka determinan dari matriks C adalah....​

Jawaban

no 18

Matriks At adalah transpose matriks A. Jika matriks C = (4/7 -1/7 -1/7 2/7) B = (4 2 2 8) dan A = C-1 maka determinan dari matriks At.B adalah...

Jawaban

No 19

Jika matriks a 2x+1 3 6x-1 5 tidak mempunyai invers.maka nilai x adalah

Jawaban

No 20

diketahui matriks a= ( 3, y, 5,-1) , b= ( x,5,-3,6), dan c = ( -3,-1, y, 9) . jika a+ b - c = ( 8, 5x, -x , -4) nilai x + 2xy + y adalah..

Jawaban

Question 4

No 21

No 22

Suatu perusahaan pakaian, JCloth, memiliki dua pabrik yang terletak di Surabaya dan Malang. Di dua pabrik tersebut, JCloth memproduksi dua jenis pakaian, yaitu kaos dan jaket. Perusahaan tersebut memproduksi pakaian yang kualitasnya dapat dibedakan menjadi tiga jenis, yaitu standard, deluxe, dan premium. Tahun kemarin, pabrik di Surabaya dapat memproduksi kaos sebanyak 3.820 kualitas standard, 2.460 kualitas deluxe, dan 1.540 kualitas premium, serta jaket sebanyak 1.960 kualitas standard, 1.240 kualitas deluxe, dan 920 kualitas premium. Sedangkan pabrik yang terletak di Malang dapat memproduksi kaos sebanyak 4.220 kualitas standard, 2.960 kualitas deluxe, dan 1.640 kualitas premium, serta jaket sebanyak 2.960 kualitas standard, 3.240 kualitas deluxe, dan 820 kualitas premium dalam periode yang sama.

JCloth

1. Tulislah “matriks produksi” dengan ordo 3 × 2 untuk masing-masing pabrik (S untuk Surabaya dan M untuk Malang), dengan kolom kaos, kolom jaket, dan tiga baris yang menunjukkan banyaknya jenis-jenis pakaian yang diproduksi.

2. Gunakan matriks dari poin 1 untuk menentukan banyaknya pakaian yang telah diproduksi oleh pabrik di Surabaya dan Malang.

3. Gunakan perkalian skalar untuk menentukan berapa banyak pakaian dari masing-masing jenis yang akan diproduksi di Surabaya dan Malang, jika perkiraan peningkatan produksinya adalah 4%.

4. Berapa total banyak pakaian yang diproduksi oleh JCloth (di kedua pabrik) pada tahun depan, untuk setiap jenis pakaian?

Jawaban

No 23

Arman membeli 5 pensil dan 3 penghapus, sedangkan susi membelu 4 pensil dan 2 penghapus di toko yang sama. Di kasir, arman membayar Rp. 11.500 sedangkan susi membayar RP. 9.000. Jika doni membeli 6 dan 5 penghapus, berapa ia harus membayar

Jawaban

x = pensil

y = penghapus

5x + 3 y = 11.500 (x2)

4x + 2 y = 9.000 (x3)

_______________

10x + 6 y = 23.000

12x + 6y = 27.000

_______________ (-)

-2x = -4.000

x = 2.000

4x + 2y = 9.000

4*2000 + 2y = 9000

2y = 1000

y = 500

jadi harga pensil = 2000 dan penghapus = 500

sehingga doni harus membayar 6*2000 + 5*500 = 12.000+2.500 = 14.500

No 24

Bu Ani seorang pengusaha makanan kecil yang menyetorkan dagangannya ke tiga kantin sekolah. Tabel banyaknya makanan yang disetorkan setiap harinya sebagai berikut. Kacang Keripik Permen Kantin A | 10 | 10 | 5 | Kantin B | 20 | 15 | 8 | Kantin C | 15 | 20 | 10 | (Dalam satuan bungkus) Harga sebungkus kacang, sebungkus keripik, dan sebungkus permen berturut-turut adalah Rp 2.000,00; Rp 3.000,00; dan Rp 1.000,00. Pertanyaan: a. Nyatakan banyaknya makanan yang disetorkan setiap harinya dengan matriks b. Nyatakan harga makanan dalam bentuk matriks c. Hitung pemasukan Bu Ani dari setiap kantin dengan cara perkalian matriks d. Carilah determinan matriks dari banyaknya makanan yang disetorkan setiap harinya

Jawaban

No 25

Lisa dan muri bekerja pada pabrik tas. Lisa dapar menyelesaikan 3 buah setiap jam dan muri dapat menyelesaikan 4 tas setiap jam jumlah jam kerja lisa dan muri adalah 16 jam sehari dengan jumlah tas yang dibuat oleh keduanya adalah 55 tas. Jika jam kerja keduanya berbeda, lisa bekerja selama x jam dan muri bekerja selama y jam, maka model matematika penyrlrsaian masalah tersebut menggunakan matriks adalah

Jawaban