materi pelajaran matematika yang disukai: September 2020

Soal Transformasi, Translasi, Refleksi, Rotasi, Dilatasi dengan Perhitungan Matriks untuk Mencari Bayangannya: Titik, Garis, Bidang Datar, dan Ruangan

contoh soal

1. persamaan peta garis 3x – 4y = 12, karena refleksi terhadap garis y – x = 0, dilanjutkan oleh

transformasi yang bersesuaian dengan matriks $\left(\begin{array}{rr} -3&5\\ -1&1\end{array}\right)$ adalah… (UAN ’03)

Pembahasan:

Diketahui matriksnya:

Rotasi = $\left(\begin{array}{rr} 0&1\\ 1&0\end{array}\right)$

Transformasi = $\left(\begin{array}{rr} -3&5\\ -1&1\end{array}\right)$

Persamaan garis direfleksi kemudian ditransformasi adalah:

$\left(\begin{array}{r} x'\\ y'\end{array}\right) = \left(\begin{array}{rr} -3&5\\ -1&1\end{array}\right) \left(\begin{array}{rr} 0&1\\ 1&0\end{array}\right) \left(\begin{array}{r} x\\ y\end{array}\right) = \left(\begin{array}{rr} 5&-3\\ 1&-1\end{array}\right) \left(\begin{array}{r} x'\\ y'\end{array}\right)$

$\left(\begin{array}{r} x\\ y\end{array}\right) = - \frac{1}{2} \left(\begin{array}{rr} -1&3 \\ -1&5\end{array} \right) \left(\begin{array}{r} x'\\ y'\end{array}\right) = \begin{pmatrix} \frac{x'-3y'}{2} \\ \frac{x'-5y'}{2} \end{pmatrix}$

Kemudian disubstitusikan:

$3x - 4y = 12 \overset{substitusi}{\rightarrow}3 (\frac{x'- 3y'}{2}) - 4(\frac{x'-5y'}{2}) = 12$

$3(x' - 3y') - 4(x'- 5y') = 24$

$3x' - 9y' - 4x' + 20y' =24$

$-x' + 11y' =24$

Hasilnya:

$11y - x =24$

2. Ditentukan matriks transformasi .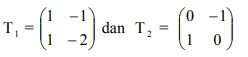 soal transformasi geometri no 5 Hasil transformasi titik (2,-1) terhadap T₁ dilanjutkan T₂ adalah….

A. (-4,3)

B. (-3,4)

C. (3,4)

D. (4,3)

E. (3,-4)

Jawaban : A

Pembahasan :

soal transformasi geometri dan jawaban no 5

3. Oleh matriks $A = \left(\begin{array}{rr} a+2&a\\ 1&a+1\end{array}\right)$ , titik $P(1, 2)$ dan titik Q masing-masing ditransformasikan ke titik $P'(2, 3)$ dan $Q'(2,0)$ . Tentukan koordinat titik Q. (SPMB’04)

Pembahasan:

Mencari nilai a dari transformasi P:

$\left(\begin{array}{r} x'\\ y'\end{array}\right)= \left(\begin{array}{rr} a+2&a\\ 1&a+1\end{array}\right) \left(\begin{array}{r} x\\ y\end{array}\right)\overset{sehingga}{\rightarrow}\left(\begin{array}{r} 2\\ 3\end{array}\right) = \left(\begin{array}{rr} a+2&a\\ 1&a+1\end{array}\right) \left(\begin{array}{r} 1\\ 2\end{array}\right)\overset{menjadi}{\rightarrow}\left(\begin{array}{r} 2\\ 3\end{array}\right) = \left(\begin{array}{rr} 2 + 3a\\ 3 + 2a\end{array}\right)$

$a = 0$

Sehingga matriksnya:

$A = \left(\begin{array}{rr} a+2&a\\ 1&a+1\end{array}\right) = \left(\begin{array}{rr} 2&0\\ 1&1\end{array}\right)$

Mencari titik Q:

$\left(\begin{array}{r} x'\\ y'\end{array}\right) = \left(\begin{array}{rr} 2&0\\ 1&1\end{array}\right) \left(\begin{array}{r} x\\ y\end{array}\right) \overset{sehingga}{\rightarrow} \left(\begin{array}{r} x\\ y\end{array}\right) = \frac{1}{2} \left(\begin{array}{rr} 1&0\\ -1&2\end{array}\right) \left(\begin{array}{r} x'\\ y'\end{array}\right) \overset{disubstitusi} = {\rightarrow} \left(\begin{array}{r} x\\ y\end{array}\right) = \frac{1}{2} \left(\begin{array}{rr} 1&0\\ -1&2\end{array}\right) \left(\begin{array}{r} 2\\0\end{array}\right)$

$\left(\begin{array}{r} x\\ y\end{array}\right) = \left(\begin{array}{r} 1\\ -1\end{array}\right)$

Sehingga:

$Q(1, -1)$

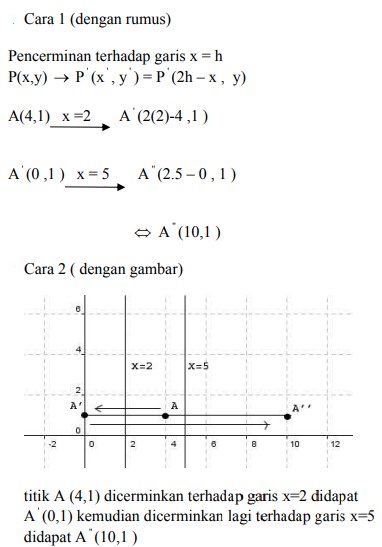
4. Bayangan titik A (4,1) oleh pencerminan terhadap garis x =2 dilanjutkan pencerminan terhadap garis x = 5 adalah titik….

A. A” (8,5)

B. A” (10,1)

C. A” (8,1)

D. A” (4,5)

E. A” (20,2)

Jawaban : B

Pembahasan :

soal transformasi geometri dan jawaban no 7

5. Persamaan garis 3x – y – 11 = 0 karena refleksi terhadap garis y = x, dilanjutkan oleh transformasi yang bersesuaian dengan matriks A,

$\begin{pmatrix} -3 & 2 \\ -1 & 1 \end{pmatrix}$

adalah ….
A. –2x – 7y –11 = 0
B. 2x + 7y – 11 = 0
C. –2x – 7y + 11 = 0
D. 2y – 7x + 11 = 0
E. 2x – 7y + 11 = 0

Pembahasan:

Pertama, cari hasil bayangan dari pencerminan terhadap garis y = x.

Matriks pencerminan terhadap garis y = x adalah:

Berdasarkan rumus di atas, dapat diperoleh kesimpulan bahwa x’ = y dan y’ = x. Substitusikan nilai tersebut pada persamaan 3x – y – 11 = 0 sehingga diperoleh persamaan berikut.

3x – y – 11 = 0
3y’ – x’ – 11 = 0
– x’ + 3y’ – 11 = 0

Kedua, langkah selanjutnya adalah transformasi yang bersesuaian dengan matriks A,

$\begin{pmatrix} -3 & 2 \\ -1 & 1 \end{pmatrix}$

Perhatikan langkah – langkahnya seperti berikut,

$\begin{pmatrix} x'' \\ y'' \end{pmatrix} = \begin{pmatrix} -3 & 2 \\ -1 & 1 \end{pmatrix} \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} -3x' + 2y' \\ -x' + y' \end{pmatrix}$

Sehingga, diperoleh dua persamaan berikut.

–3x’ + 2y’ = x’’
– x’ + y’ = y’’

Berikutnya, akan dicari persamaan yang senilai dengan x’ dan y’:

Mencari nilai x’:

Metode eliminasi variabel

Mencari nilai y’:

Metode eliminasi variabel

Subtitusi hasil x’ dan y’ di atas pada persamaan – x’ + 3y’– 11 = 0:

$-x' + 3y' - 11 = 0$

$-\left( 2y'' - x'' \right) + 3\left( 3y'' - x'' \right) - 11 = 0$

$-2y'' + x'' + 9y'' - 3x'' - 11 = 0$

$-2x'' + 7y'' - 11 = 0$

$2x'' - 7y'' + 11 = 0$

Jadi, hasil akhir transformasi dari persamaan 3x – y – 11 = 0 adalah 2x – 7y + 11 = 0.

Jawaban: E

6. Bayangan ∆ABC dengan A(2,1), B(6,1), C(5,3) karena refleksi terhadap sumbu y dilanjutkan rotasi (0,90°) adalah…

A. A” (-1,-2), B” (1,6) dan C” (-3,-5)

B. A” (-1,-2), B” (1,-6) dan C” (-3,-5)

C. A” (1,-2), B” (-1,6) dan C” (-3,5)

D. A” (-1,-2), B” (-1,-6) dan C” (-3,-5)

E. A” (-1,2), B” (-1,-6) dan C” (-3,-5)

Jawaban : D

Pembahasan :

soal transformasi geometri dan jawaban no 9

7. Dilatasi yang berpusat di titik (3, 1) dengan faktor skala 3, memetakan titik (5, b) ke titik (a, 10). Maka nilai a – b adalah ….
A. 15
B. 11
C. 5
D. 4
E. 2

Pembahasan:

Dilatasi dengan pusat (3, 1) dengan faktor skala 3 akan menghasilkan matriks transformasi berikut.

$\begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} 3 & 0 \\ 0 & 3 \end{pmatrix} \begin{pmatrix} 5 - 3 \\ b- 1 \end{pmatrix} + \begin{pmatrix} 3 \\ 1 \end{pmatrix}$

$\begin{pmatrix} a \\ 10 \end{pmatrix} = \begin{pmatrix} 3 & 0 \\ 0 & 3 \end{pmatrix} \begin{pmatrix} 2 \\ b- 1 \end{pmatrix} + \begin{pmatrix} 3 \\ 1 \end{pmatrix}$

$\begin{pmatrix} a \\ 10 \end{pmatrix} = \begin{pmatrix} 6 \\ 3b - 3 \end{pmatrix} + \begin{pmatrix} 3 \\ 1 \end{pmatrix}$

$\begin{pmatrix} a \\ 10 \end{pmatrix} = \begin{pmatrix} 9 \\ 3b - 2 \end{pmatrix}$

Sehingga dapat diperoleh nilai a dan b:

a = 9
3b – 2 = 10
3b = 12
b = 12 : 3 = 4

Jadi, nilai a – b = 9 – 4 = 5

Jawaban: C

8. Segitiga ABC dengan A(2,1), B(6,1), C(6,4) ditransformasikan dengan matriks transformasi 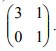soal transformasi geometri no 12 Luas bangun hasil transformasi segitiga ABC adalah….

A. 56 satuan luas

B. 36 satuan luas

C. 28 satuan luas

D. 24 satuan luas

E. 18 satuan luas

Jawaban : E

Pembahasan :

misalkan T = 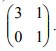soal transformasi geometri no 12 maka

Luas bayangan/transformasi ∆ ABC =|det T| x luas ∆ ABC |det T| = |ad –bc| = |3-0| = 3

luas ∆ ABC :

buat sketsa gambar :

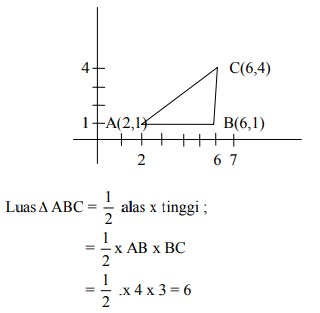
soal transformasi geometri dan jawaban no 12

Luas bayangan/transformasi ∆ ABC =|det T| x luas ∆ ABC

= 3 x 6 = 18 satuan luas

1. Transformasi atau nama lengkapnya Transformasi Geometri adalah perubahan posisi atau perpindahan dari posisi awal P(x, y) ke posisi lain P'(x', y'). Nah perubahan posisi ini bisa disebabkan oleh 4 hal:

Translasi atau pergeseran
Refleksi atau pencerminan
Rotasi atau perputaran
Dilatasi atau perkalian yang mengakibatkan bidang geometri mengalami perbesaran atau pengecilan.

a. Translasi atau pergeseran adalah bentuk transformasi geometri yang tidak mengubah bentuk dan ukuran, hanya mengubah posisi ke kiri, kanan, atas dan atau bawah.

Beberapa hal yang perlu diingat tentang konsep translasi yaitu:

Pergeseran ke kanan atau ke kiri hanya mempengaruhi variabel x
Pergeseran ke atas atau ke bawah hanya mempengaruhi variabel y
Pergeseran ke kanan atau atas tandanya negatif (-)
Pergeseran ke kiri atau bawah tandanya positif (+).

Ingat saja diagram kartesius :)

Rumus praktis translasi oleh T(a, b) adalah

b. Pencerminan atau refleksi adalah salah satu jenis transformasi geometri yang akan memetakan suatu titik pada bangun geometri dengan menggunaan sifat benda dan bayangan pada cermin datar. Bayangan hasil pencerminan akan memiliki bentuk dan ukuran yang sama dengan bentuk dan ukuran awalnya.

Rumus Pencerminan Terhadap Sumbu X:

Rumus Pencerminan Terhadap Sumbu Y:

Rumus Pencerminan Terhadap Titik Pusat O(0, 0):

Rumus Pencerminan Terhadap Titik (a, b):

Rumus Pencerminan Terhadap Garis x = y:

Rumus Pencerminan Terhadap Garis x = -y atau -x = y:

Rumus Pencerminan Terhadap Garis x = a:

Rumus Pencerminan Terhadap Garis y = a:

c. Dilatasi : Perbesaran atau pengecilan suatu objek berdasarkan skala yang telah ditentukan. Dalam geometri transformasi, dilatasi dapat dirumuskan dengan perkalian matriks.

A adalah titik (Ax,Ay), P adalah pusat titik (Px,Py), dan S adalah faktor skala.

A' = ( S 0 ) ( Ax-Px ) + ( Px )

( 0 S ) ( Ay-Py ) ( Py )

Dilatasi menurut jenis skalanya dibagi menjadi dua, yaitu dilatasi pembesaran (dimana S>1) dan pengecilan (dimana 0<S<1).

d. Rotasi (perputaran) : Perputaran suatu objek dengan bertumpu pada suatu titik pusat sejauh nilai derajatnya yaitu 0 sampai 360 derajat. Dalam geometri transformasi, rotasi dapat dirumuskan dengan perkalian dan penjumlahan matriks.

A adalah titik (Ax,Ay), P adalah matriks untuk rotasi dengan menggunakan rumus trigonometri yaitu sin dan cos, dan α adalah besarnya sudut suatu rotasi yang dinyatakan dengan derajat (°). Rumus ini berlaku selama titik pusatnya adalah O (0,0).

A' = P * A = ( cos α sin α ) ( Ax )

( -sin α cos α ) ( Ay )

Rotasi dapat dibagi menjadi 2, yaitu arah jarum jam (ke kanan) dengan nilai positif dan berlawanan arah jarum jam (ke kiri) dengan nilai negatif.

Transformasi Translasi, Refleksi, Rotasi dan Dilatasi dengan gambar balok ABCDEFGH koordinat titik A(0,0), B(4,0), C(4,4), D(0,4), E(10,0), F(14,0), G(14,4), H(10,4) dan perhitungan mendapat bayangannya

materi pelajaran matematika yang disukai

Sunday, September 27, 2020

TRANSFORMASI TRANSLASI, REFLEKSI, ROTASI, DILATASI DENGAN MATRIKS

Monday, September 21, 2020

TRANSFORMASI TRANSLASI, REFLEKSI, ROTASI, DILATASI DENGAN GAMBAR DAN PERHITUNGANNYA

Remedial PAT

Report Abuse