Nama : M. Aydin Ramadhan
Kelas : XI IPS 2
Absen : 20
20.
PERTUMBUHAN, BUNGA TUNGGAL, BUNGA MAJEMUK, BUNGA ANUITAS, PELURUH DAN BEBERAPA CONTOH SOAL
Diketahui modal pinjaman Rp1.000.000 dengan bunga sebesar per bulan, maka setelah 5 bulan modalnya adalah ….
Pertumbuhan merupakan kenaikan jumlah pada tiap periode waktu berdasarkan suatu rasio pertumbuhan. Jika jumlah awal adalah dan rasio adalah r per tahun, maka pada akhir tahun ke-n, jumlah akhirnya menjadi
:
Contoh, jumlah penduduk 10.000 jiwa dengan pertumbuhan penduduk 5% per tahun, maka pada akhir tahun ke-4, jumlahnya
Penyusutan atau depresiasi adalah pengurangan nilai dari harta tetap terhadap nilai buku atau nilai beli awalnya. Penyusutan dilakukan secara berkala dalam rangka pembebanan biaya pada pendapatan, baik atas penggunaan harta tersebut maupun karena sudah tidak memadai lagi.
Jika harga sebuah barang pada saat dibeli adalah dan mengalami penyusutan tiap tahunnya sebesar p (dalam persen) dari harga belinya, maka nilai barang pada akhir tahun ke-n adalah :
Contoh, harga mobil Rp100.000.000 menyusut harganya 10% tiap tahun. Di akhir tahun ke-5 nilainya
1. Diketahui premis-premis berikut :
Premis 1 = Jika masyarakat membuang sampah pada tempatnya maka lingkungan bersih
Premis 2 = Jika lingkungan bersih maka hidup akan nyaman
simpulan yang sah dari kedua premis tersebut adalah
Jika masyarakat membuang sampah pada tempatnya maka hidup akan jadi nyaman
2.
9. diket :
5kg gula + 30kg beras = 410.000
2kg gula + 60kg beras = 740.000
Dit : 2kg gula + 5kg beras ?
Jwb :
gula = x
beras = y
5x + 30y = 410.000 |*2
2x + 60y = 740.000 |*1
10x + 60y = 820.000
2x + 60y = 740.000
_______-
8x = 80.000
x = 10.000
subtitusikan x nya ke persamaan
2x + 60y = 740.000
2(10.000) + 60y = 740.000
20.000 + 60y = 740.000
60y = 720.000
y = 12.000
jadi, harga 1kg gula = Rp 10.000 dan 1kg beras = Rp 12.000
maka 2kg gula dan 5kg beras
= 2(10.000) + 5(12.000)
= 20.000 + 60.000
= Rp 80.000
10. tentukan daerah bersih dari pertidaksamaan linear berikut 5x + 3y ≤ 15
jawaban :
5x + 3y ≤ 15 uji 0
x = 0 | x = 0 5(0) + 3(0) ≤ 15
y = 5 | y = 3 0 ≤ 15 (benar)
11. 2x - 5y > 20
Cara penyelesaian :
a. Mencari x dan y
x 0 10
y -4 0
b. Menentukan dan letak daerah kotor
2(0) - 5(0) > 20
0 > 20 (salah)
c. Membuat garis koordinat
12.
5x + 6y ≥ 30 (0,5) (6,0) *karena a positif dan tanda ≥ maka daerahnya berada di kanan garis
2x + y ≤ 0 (0,0) (0,0) *karena a negatif dan tanda ≤ maka daerahnya berada di kanan garis
Y ≥ 2 *daerah berada pada rentang y ≥ 2, y € r
Maka daerah penyelesaian dari model mtk tsb berada di daerah III
13. Daerah yang diarsir pada gambar adalah himpunan penyelesaian dari sistem pertidaksamaan 3x + 5y ≤ 30 ; 2x - y ≤ 4 ; x ≥ 0 dan y ≥ 0.
Penyelesaian Soal :
LANGKAH PERTAMA (I)
Buatlah sistem pertidaksamaan pada setiap garis dengan menggunakan cara sebagai berikut :
Persamaan garis I melalui titik (0,6) dan (10,0) sehingga :
ax + by = ab
6x + 10y = 6.10
6x + 10y = 60 .... (÷2)
3x + 5y = 30
Kemudian perhatikan daerah arsiran yang mengarah ke bawah atau melalui titik (0,0). Jika arsiran melalui titik (0,0) maka jika diuji titik (0,0) pernyataan dikatakan benar :
3x + 5y = 30
3.0 + 5.0 = 30
0 + 0 = 30
0 ≤ 30 (Benar)
Pertidaksamaannya : 3x + 5y ≤ 30
Persamaan garis II melalui titik (0,-4) dan (2,0) sehingga :
ax + by = ab
-4x + 2y = (-4).2
-4x + 2y = -8 .... (÷ 2)
-2x + y = -4
Kemudian perhatikan daerah arsiran yang mengarah ke sisi kiri atau melalui titik (0,0). Jika arsiran melalui titik (0,0) maka jika diuji titik (0,0) pernyataan dikatakan benar :
-2x + y = -4
(-2).0 + 0 = -4
0 + 0 = -4
0 ≥ -4 (Benar)
Pertidaksamaannya :
-2x + y ≥ -4 .... (× -1)
2x - y ≤ 4
Kemudian pada arsiran juga terdapat garis x ≥ 0 dan y ≥ 0.
Sehingga pertidaksamaannya adalah :
3x + 5y ≤ 30 ; 2x - y ≤ 4 ; x ≥ 0 dan y ≥ 0.
14. Nilai Maksimum 3x + 2y ?
x + y > 5
sumbu x ; y = 0 ( 5, 0)
sumbu y ; x = 0 ( 0, 5)
maka Nilai Maksimumnya adalah
3x + 2y
( 5, 0) = 3(5) + 2(0) = 15
(0, 5) = 3(0) + 2(5) = 10
Nilai maksimum nya adalah 15
15.Diketahui=
X = banyaknya sedan
Y = banyaknya truk
Luas Parkiran:
sedan= 15
Truk = 15
Kapasitas 420
Kuantitas:
sedan= 1
Truk = 1
Kapasitas 60
Jawab:
•Persamaan garis 1 : 5x + 15y = 4200
Titik (0,0) merupakan salah satu himpunan penyelesaian dari
pertidaksamaan tersebut sehingga diperoleh
5x + 15y = 4200 disederhanakan menjadi
5x + 15y ≤ 4200
•Persamaan garis 2 : x + y = 60
Titik (0,0) merupakan salah satu himpunan penyelesaian dari
pertidaksamaan tersebut sehingga diperoleh
x + y = 60 disederhanakan menjadi
x + y ≤ 60
•Kendala non negative diberikan oleh
X ≥ 0, y ≥ 0
•Jadi model matematika nya
5x + 15y ≤ 4200; 4x + y ≤ 60 ; x ≥ 0, y ≥ 0
Jawaban: 5x + 15y ≤ 4200; 4x + y ≤ 60 ; x ≥ 0, y ≥ 0
16. diket :
- Model I memerlukan 1 m kain polos dan 3 m kain bergaris.
- Model II memerlukan 2 m kain polos dan 1 m kain bergaris.
- Persediaan kain polos 20 m
- persediaan kain bergaris 20 m
- Harga jual model I Rp.150.000,00
- Harga jual model II Rp.100.000,00
Dit : Penghasilan maksimum yang dapat diperoleh = ...
Jwb :
(1) Kita Buat Tabel Untuk memudahkan:
Model || Polos || Garis || Harga
I || 1 || 3 || 150.000
II || 2 || 1 || 100.000
Stok || 20 || 20 || maksimum
(2) Kita buat kalimat matematika dari Tabel diatas Dengan kain polos sebagai (x) dan kain bergaris sebagai (y) :
x + 2y ≤ 20
3x + y ≤ 20
dengan :
x ≥ 0
y ≥ 0
Dan Fungsi Tujuan adalah harga jual :
150.000x + 100.000y
(3) Tentukan nilai fungsi x dan y pada grafik fungsi :
Dari x + 2y = 20 :
x = 0, y ⇒ 0 + 2y = 20
⇒ 2y = 20
⇒ y = 20/2
⇒ y = 10
Titik Koordinat ⇒ (0,10)
y = 0, x ⇒ x + 2y = 20
⇒ x + 0 = 20
⇒ x = 20
Titik Koordinat ⇒(20,0)
Dari 3x + y = 20
x = 0 , y ⇒ 3x + y = 20
⇒ 0 + y = 20
Titik Koordinat ⇒ (0,20)
y = 0, x ⇒ 3x + y = 20
⇒ 3x + 0 = 20
⇒ 3x = 20
⇒ x = 20/3
Titik Koordinat ⇒ (20/3,0)
Dari Titik - titik tersebut tarik garis lurus hingga terhubung.
Lalu kita cari titik potong dari garis tersebut, dengan metode eliminasi dan subtitusi :
Eliminasi y :
x + 2y = 20 | x 1 | x + 2y = 20
3x + y = 20 | x 2 | 6x + 2y = 40
============ -
-5x = -20
x = 20/5
x = 4
Subtitusikan nilai x pada persamaan 3x + y = 20 :
3 . 4 + y = 20
12 + y = 20
y = 20 - 12
y = 8
Koordinat titik potong garis pada (4,8)
(4) Selanjutnya Dari Titik - titik yang berpotongan kita uji dengan :
Fungsi Tujuan f(x,y) = 150.000x + 100.000y :
Ada 3 titik pada Grafik (perhatikan lampiran)
A. Titik (0,10) = 150.000 . (0) + 100.000 . (10) =
= 0 + 1.000.000 = 1.000.000
B. Titik (4,8) = 150.000 . (4) + 100.000 . (8) =
= 600.000 + 800.000 = 1.400.000
C. Titik (20/3,0) = 150.000 . (20/3) + 100.000 . (0) =
= 1.000.000 + 0 = 1.000.000
Dari Hasil Uji diatas dapat dilihat, penghasilan terbesar pada titik (4,8) yaitu sebesar Rp.1.400.000,00
17.
18.

A =
Matriks A tidak mempunyai invers
Ditanyakan
x = .... ?
Jawab
Suatu matriks tidak mempunyai invers jika determinan matriks tersebut sama dengan nol
|A| = 0
(2x + 1)(5) – 3(6x – 1) = 0
10x + 5 – 18x + 3 = 0
8 – 8x = 0
8 = 8x
x =
x = 1
20.
21.
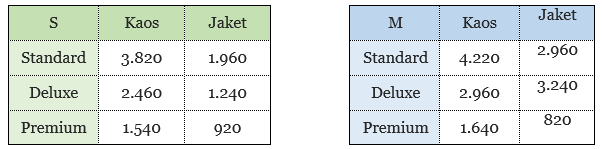
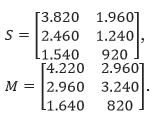
Untuk menentukan banyaknya total pakaian yang diproduksi oleh JCloth, kita jumlahkan matriks S’ dengan M’ seperti berikut.
Dari penjumlahan matriks di atas, kita memperoleh informasi banyaknya pakaian yang akan diproduksi oleh JCloth. Dengan menjumlahkan semua elemen-elemen matriks penjumlahan tersebut, kita peroleh bahwa banyaknya pakaian yang akan diproduksi oleh JCloth kurang lebih 28.142.
23. pensil (x) dan penghapus (y)
Maka:
24. Banyaknya makanan yang disetorkan setiap harinya adalah,
25.
x + y = 16
3x + 4y = 551. Translasi (pergeseran)
Translasi adalah perubahan objek dengan cara menggeser objek dari satu posisi ke posisi lainnya dengan jarak tertentu.
2. Refleksi (pencerminan)
3. Rotasi (perputaran)
Rotasi atau perputaran adalah sebuah perubahan kedudukan objek dengan cara diputar melalui pusat dan sudut tertentu.
4. Dilatasi (perbesaran)
Refleksi merupakan salah satu bagian dari transformasi geometri, dimana benda yang kita refleksikan akan berlawanan arah dengan benda aslinya.
Pencerminan terhadap sumbu x
A(a, b) → sb x → A'(a, -b)
Pencerminan terhadap sumbu y
A(a, b) → sb y → A'(-a, b)
Pencerminan terhadap garis y = x
A(a, b) → gr y = x → A'(b, a)
Pencerminan terhadap garis y = -x
A(a, b) → gr y = -x → A'(-b, -a)
Pencermianan terhadap titik pangkal koordinat
A(a, b) → titik pangkal → A'(-a, -b)
Pencerminan terhadap garis x = h
A(a, b) → garis x = h → A' (2h - a, b)
Pencerminan terhadap garis y = k
A(a, b) → garis y = k → A'(a, 2k - b)
Bayangan titik A (-1, 4) oleh refleksi terhadap garis y= -x
Pencerminan terhadap garis y = -x
A(a, b) → gr y = -x → A'(-b, -a)
A(-1, 4) → gr y = -x → A'(-4, -(-1)) = (-4, 1)
27. (x, y) dicerminkan thp sumbu x : (x, -y) kemudian
Step-1 pencerminan garis x = k
Untuk x = 2
(x' , y') = (2(2) - x, y)
(x' , y') = (4 - x, y) akan disubtitusi ke Step-2
Step-2 translasi (- 3, 4)
Translasi (a, b) dengan a = -3 dan b = 4.
(x", y") = (x' + (- 3), y' + 4)
(x", y") = (4 - x + (- 3), y + 4)
(x", y") = (1 - x, y + 4)
Sehingga, x" = 1 - x dan y" = y + 4
Setelah diatur dengan pindah ruas menjadi
Substitusikan ke bentuk awal x²+ y² = 4
⇔ (1 - x")² + (y" - 4)² = 4
Selanjutnya tanda aksen dapat dihilangkan
⇔ (1 - x)² + (y - 4)² = 4
⇔ x² - 2x + 1 + y² - 8y + 16 = 4
⇔ x² + y² - 2x - 8y + 1 + 16 - 4 = 0
Dari langkah-langkah pengerjaan di atas, diperoleh persamaan bayangan lingkaran
30. A(3,-2)
dipetakan oleh T(1 -2)x' = x
y' = -y
Bayangan
y = x² + 3x + 3
-y' = x'² + 3x' + 3
y = -x² - 3x - 3
• lanjut dilatasi [O, 4]
x' = 4x → x = 1/4 x'
y' = 4y → y = 1/4 y'
Bayangan akhir
y = -x² - 3x - 3
1/4 y' = -(1/4 x')² - 3(1/4 x') - 3
1/4 y = -1/16 x² - 3/4 x - 3
Kedua ruas kalikan 4
y = -1/4 x² - 3x - 12 ✔
33.